Perceptual quantizer

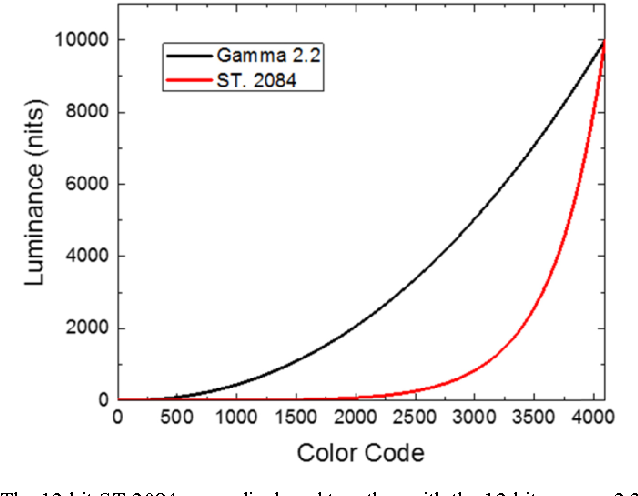
The perceptual quantizer (PQ), published by SMPTE as SMPTE ST 2084, is a transfer function that allows for HDR display by replacing the gamma curve used in SDR. It is capable of representing luminance level up to 10000 cd/m² (nits) and down to 0.0001 nits. It was developed by Dolby and standardized in 2014 by SMPTE and also in 2016 by ITU in Rec. 2100. ITU specifies the use of PQ or HLG as transfer functions for HDR-TV. PQ is the basis of HDR video formats (such as Dolby Vision, HDR10 and HDR10 ) and is also used for HDR still picture formats. PQ is not backward compatible with the BT.1886 EOTF (i.e. the gamma curve of SDR), while HLG is compatible.

PQ is a non-linear transfer function based on the human visual perception of banding and is able to produce no visible banding in 12 bits. A power function (used as EOTFs in standard dynamic range applications) extended to 10000 cd/m² would have required 15 bits.

Technical details

The PQ EOTF (electro-optical transfer function) is as follows:

$F_{D}=EOTF[E']=10000\left({\frac {\max[(E'^{1/m_{2}}-c_{1}),0]}{c_{2}-c_{3}\cdot E'^{1/m_{2}}}}\right)^{1/m_{1}}$

The PQ inverse EOTF is as follows:

$E'=EOTF^{-1}[F_{D}]=\left({\frac {c_{1} c_{2}\cdot Y^{m_{1}}}{1 c_{3}\cdot Y^{m_{1}}}}\right)^{m_{2}}$

where

$E'$ is the non-linear signal value, in the range $\left[0,1\right]$ .
$F_{D}$ is the displayed luminance in cd/m²
$Y=F_{D}/10000$ is the normalized linear displayed value, in the range [0:1] (with $Y=1$ representing the peak luminance of 10000 cd/m²)
$m_{1}={\frac {2610}{16384}}={\frac {1305}{8192}}=0.1593017578125$
$m_{2}=128{\frac {2523}{4096}}={\frac {2523}{32}}=78.84375$